First Generation of Neural Networks: Perceptrons

We will look into how perceptrons are structured and what they actually do. Perceptrons are the first generation of neural networks. Research on perceptrons was conducted since 1960s.

Network Architecture Types

Feed-forward network

  • Information flows from the input layer in one direction to the output layer
  • "deep" neural network term is used to indicate existing of more than one hidden layer.

[caption id="attachment_1312" align="aligncenter" width="277"]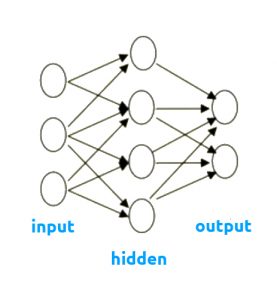feed-forward-network Feed-forward Neural Network[/caption]

Recurrent neural network

  • Information can flow around in cycles
  • They are more biologically realistic
  • Difficult to train
  • Are able to remember information in the hidden state

In 2011 Ilya Sutskever designed a recurrent neural network which was generating one character at a time.

[caption id="attachment_1317" align="aligncenter" width="292"]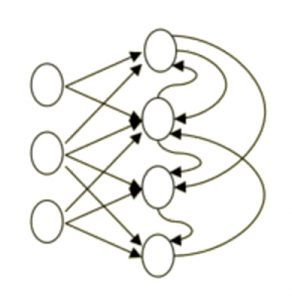recurrent-neural-network Recurrent Neural Network[/caption]

Symetrically connected network

  • Similar to recurrent networks
  • They have symmetrical connections between units (same weight in both directions)
  • Easier to analyze than recurrent networks

Perceptrons

  • Perceptrons are the first generation of neural networks
  • Have some limitation (published in 1969 Minsky and Papert, "Perceptrons" book)
  • Is still widely used today for tasks with huge feature vectors, containg many million of features.
  • Binary threshold unit is used as a decision unit

Statistical Pattern Recognition Approach:

  • convert raw input into a vector or feature activations
  • learn how to weight each feature activation to get a single scalar quantity
  • if this quantity is above a certain threshold, we decide that the input vector is a positive example of a target class

[caption id="attachment_1346" align="aligncenter" width="300"]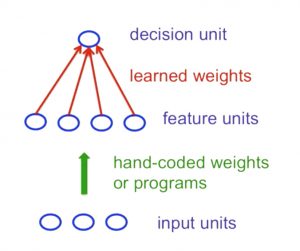perceptron-architecture Standard Perceptron Architecture[/caption]

Binary Threshold Neurons (with bias)

\begin{equation} z = b + \sum_{i}{x_i w_i} \end{equation}

\begin{equation} y =  \begin{cases} 1,  if  z \geq $\Theta$ \\ 0, otherwise \end{cases} \end{equation}

z - total input calculation
y - output of the neuron

[caption id="attachment_1166" align="aligncenter" width="322"]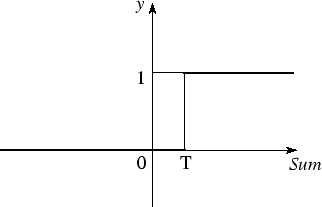binarythresholdneurons Binary Threshold Neuron[/caption]

Learning biases

Biases can be treated like weight, and can be trained accordingly. We can provide input "1" to the "bias neuron" and include it in training like any other neuron.

[caption id="attachment_1366" align="aligncenter" width="300"]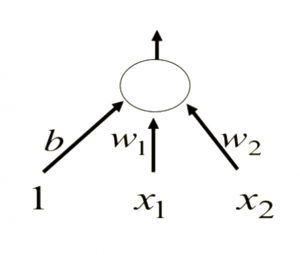binary-threshold-neuron-bias-training Binary Threshold Neuron - Training Biases[/caption]

Training Perceptrons

Using this training algorithm it is guaranteed that the right answer will be found for each training case if any such set exists.

  • add extra component with the constant value of "1" to the input vector. The weight of this component is minus the threshold.
  • pick the training cases using policy which makes sure that every training case will keep getting picked (i.e. don't change as we go)
    • output unit correct: leave its weights
    • output unit incorrecly outputs to "0": add the input vector to the weight vector
    • output unit incorrectly outputs to "1": subtract the input vector from the weight vector

Geometrical View

If we would imagine the weight space as n-dimensional space where each dimension corresponds to the value of a certain weight, then a point in this space would represent a set of weight values. Training cases in this sense would correspond to the planes.

  1. Considering a training case in which the correct answer is one, the weight vector needs to be on the correct side of hyperplane in order to get the answer right. Having the weight vector on the same side as input vector, means the angle between these two should be less than 90 degrees, implies that the scaler product on the input vector with a weight vector will be positive.
    When the weight vector is on the wrong side of the plane, the angle of the weight vector and the input vector will be negative, and the scalar product will be less than zero and we will get a wrong answer.
  2. Looking from the other perspective: for any input vector with the correct answer = 0, any weight vector which lies on the angle of < 90 with the input vector, will cause a positive scalar product, causing the answer to be = 1. This weight vector is considered bad. All "good weights" vectors are vectors which have angle to input vector > 90.

Inputs can be thought of as constains. This means that inputs constrain the set of weights that give the correct classification results by paritioning the space into two halves.

There are mathematics proofs that learning of perceptrons would lead to a feasible space if there is any feasible space.

 

Limitations of Perceptrons

Binary threshold neurons cannot sometimes satisfy easiest cases:

1. Cases that are not linearly separable

Imagine the case of sets of 2D inputs, where we want to classify the same feature inputs. In these terms, the points (0,0) and (1,1) should lead to the answer = 1, while (0,1) and (1,0) would lead to the answer = 0. In this example, there's no single set of weights which would satisfy all the constraints.

We can notice that there's a set of training cases which are not linearly separable and would lead to non-existence of weight plane which can properly classify the input.

2. Translations with wrap-arounds

Another case which perceptrons could not resolve is the case of discrimination of simple patterns when you translate them with wrap-around.

Based on this, Minskys and Papert's paper "Group Invariance Theorem" (1960s) says that the part of a Perceptron that learns cannot learn to do this if the transformations form a group. (Translations with wrap-around form a group)

Networks withou hidden units are very limited in what they can learn to model. What is required is multiple layers of adaptive, non-linear hidden units. We need the way to adapt all the weights, and not just the last layer.