What are Neural Networks? Why do we use them?
Why do we use neural networks?
Neural networks help us solve a lot of complicated problems when there’s no clear way to solve it. Sometimes problems can be complicated enough where we don’t know how to solve it, or solving them in conventional way will lead to very complicated algorithms which cannot adapt to changes.
Neural networks play essential role in acting like human brain - helping us solving problems which we are good at: speech recognition, object recognition, pattern recognition, classification, etc…
Neural networks consists of layers on neurons, starting from input layer - which accepts the signal from receptors - one or multiple hidden layers (quite a big amount of hidden layers is one of main characteristics of deep learning networks) and output layer. Neurons of each layer are interconnected with the neurons next layer through synapses - which act like connectors transmitting signals. These synapses have positive or negative weights which will inhibit (negative weight) or excite (positive weight) neurons. Incoming signals from synapses are combined within the neuron and are passed through outgoing synapses to the next layer neural connections. Adjusting synaptical weights gives the ability to the neural network to respond to experience.
MNIST - is a database of handwritten digits which is publicly available and can be used to train our networks.
ImageNet task - is a competition of classification of 1.3 million high resolution images from the web into 1000 different object classes. Measurements are done on top-1 and top-5 error rates. Top-1 error rate - error rate of classification of image matching the first answer of classification of machine. Top-5 error rate - error rate of classification of image being one of the top 5 choices selected by machine.
Speech Recognition - improved drastically with introduction of deep neural networks. Google achieved 12.3% error rate in android 4.1 after 5,870 hours of training data.
Neuron Models
Linear Neurons
This is the simplest model for a neuron.
\begin{equation} y = b + \sum_{i}{x_i w_i} \end{equation}
$b$ - bias for the neuron
$i$ - index of input connection to neuron i
$x_i$ - $i^{th}$ input
$w_i$ - weight on $i^{th}$ input
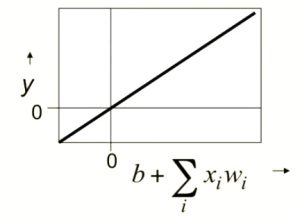
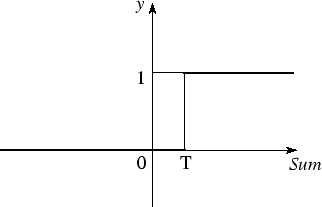
Binary Threshold Neurons
\begin{equation} z = \sum_{i}{x_i w_i} \end{equation}
\begin{equation} y = \begin{cases} 1, if z \geq \Theta \\ 0, otherwise \end{cases} \end{equation}
z - total input calculation
y - output of the neuron
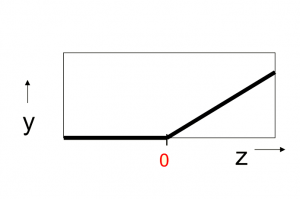
Rectified Linear Neurons (Linear Threshold Neurons)
\begin{equation} z = \sum_{i}{x_i w_i} \end{equation}
\begin{equation} y = \begin{cases} z, if z \geq 0 \\ 0, otherwise \end{cases} \end{equation}
z - total input calculation
y - output of the neuron
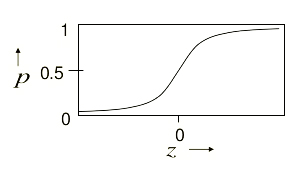
Sigmoid Neurons
\begin{equation} z = b + \sum_{i}{x_i w_i} \end{equation}
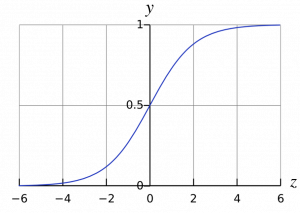
\begin{equation} y = \dfrac{1}{1 + e^{-z}} \end{equation}
z - total input calculation
y - output of the neuron
The beauty about the neuron is that it will generate an output betwen 0 and 1. with higher $z$ you will get $y$ approaching 1, while the lower, negative $z$ will lead to $y$ approaching 0.
Stochastic Binary Neurons
Use the same equations of logistic units. The output of logistic is treated as the probability of producing a spike.
\begin{equation} z = b + \sum_{i}{x_i w_i} \end{equation}
\begin{equation} p(s = 1) = \dfrac{1}{1 + e^{-z}} \end{equation}
z - total input calculation
s - spike
p - probability of producing 1
For example, if p(s=1) = 0.9, neuron will be giving us 1 for 90% of the times. This gives some intrinsically random nature to the neuron.